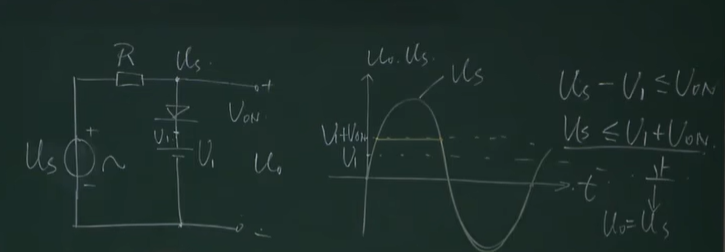模拟电子技术基础笔记
常用半导体器件
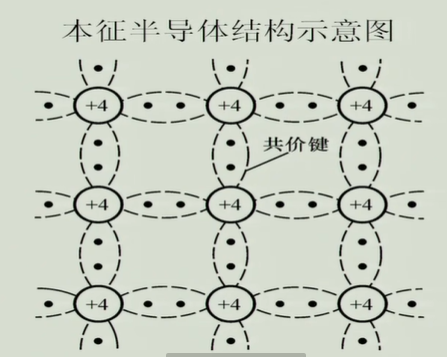
本征半导体
-
半导体:介于导体与绝缘体之间的
-
载流子 3.1 本征激发
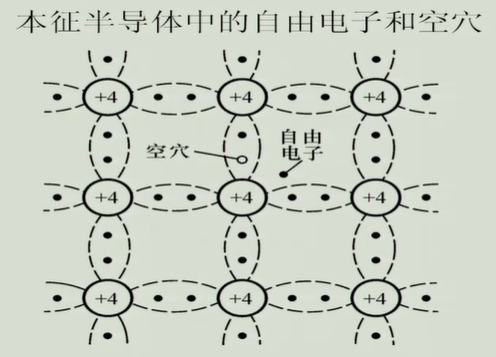
 3.2 自由电子,带负电
3.3 空穴,带正电
自由电子和空穴都能到点。
3.4 复合:与本真激发相反的过程
3.2 自由电子,带负电
3.3 空穴,带正电
自由电子和空穴都能到点。
3.4 复合:与本真激发相反的过程 -
本征半导体的导电能力与载流子的浓度有关:此时处于动态平衡,本证激发与复合的速度一样。
从工程的角度看,只加热温度让导电能力增加不实际,还好它具有掺杂别的东西让导电能力增加。
杂质半导体
概念
掺杂少量 的杂志元素。
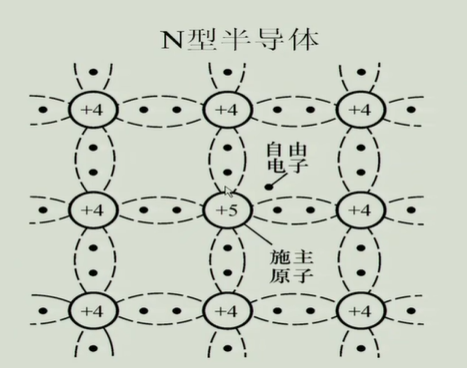
N型半导体
掺杂P元素(5价元素),本征半导体的导电能力增加,自由电子是多子,空穴是少子;
温度对多子影响小,因为多子本身就多,但对少子浓度的影响大,因为少子的量少;
P型半导体
掺杂硼元素(3价元素),本征半导体的导电能力增加,自由电子是少子,空穴是多子;
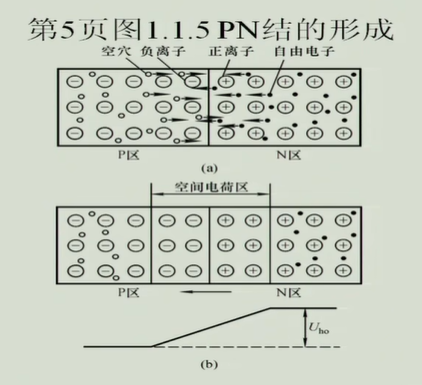
PN结半导体
1.扩散运动:在浓度梯度的作用下,浓度高的地方向浓度低的地方扩散;
2.空间电荷区(耗尽层、PN结),这里举个例子,就右边空间电荷区的正电荷而言,从电场线出发,两边平衡我们可以理为正电荷发出的电场阻止了左边的空穴移动,而对于负电荷他也有这样的特性,所以两边达到平衡的状态。
虽然中间有空间电荷区形成势垒(由电压形成)组织了两遍的多子运动,但是这样的势垒能百分之百阻止多子向两边运动吗?
答案是不完全,还是有一小部分的多子冲破避雷向两边运动。下面是一张简单的图。
3.漂移运动:两边少子的运动称之为漂移运动
4.对称结与不对称结:由上面的图可以看出两边宽度一样,原因是掺杂的浓度一样,如果不一样?那么两边就不对称了,这时候称之为不对称结。
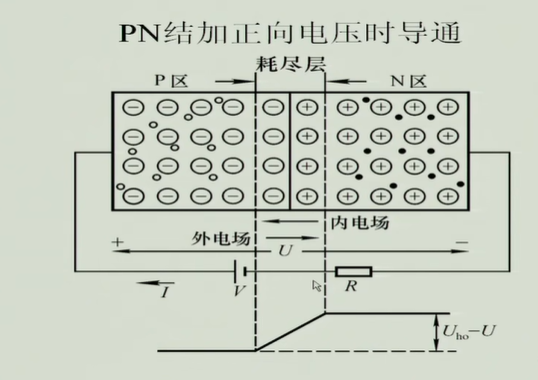
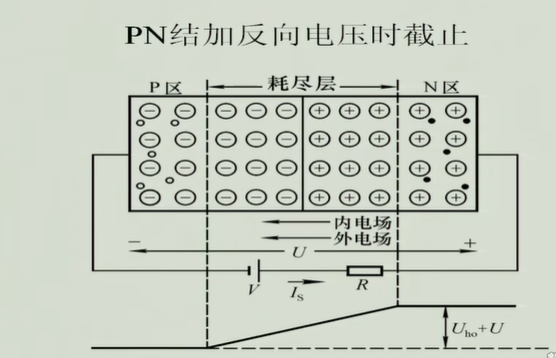
加外电压的PN结半导体
这个时候的漂移运动是增加的,但漂移运动是由少子形成的所以他的影响是很小的,值得注意的是漂移运动对 温度 是很敏感的。
PN结的电流方程
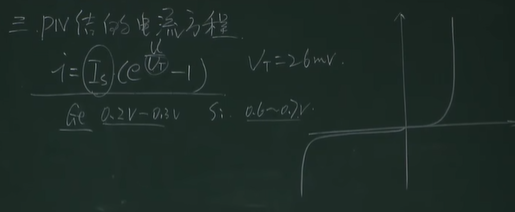
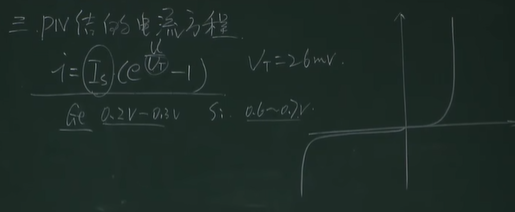 $i=I_s(e^{U/U{_T}}-1),其中V_T=26V$
$i=I_s(e^{U/U{_T}}-1),其中V_T=26V$
锗:0.2-0.3V 硅:0.6-0.7V
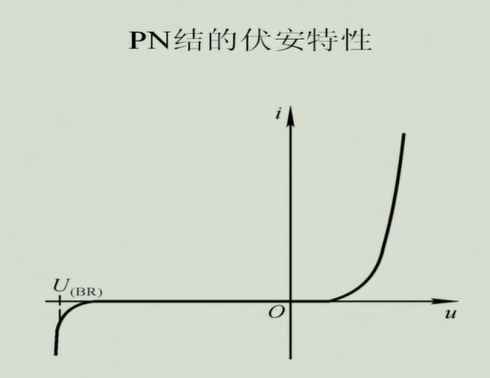
特性
- 正向特性
- 反向特性 2.1雪崩击穿(掺杂浓度低,温度越高,击穿电压越高,因为粒子需要加速) 2.2齐纳击穿(掺杂浓度高,温度越高,击穿电压越低,因为)
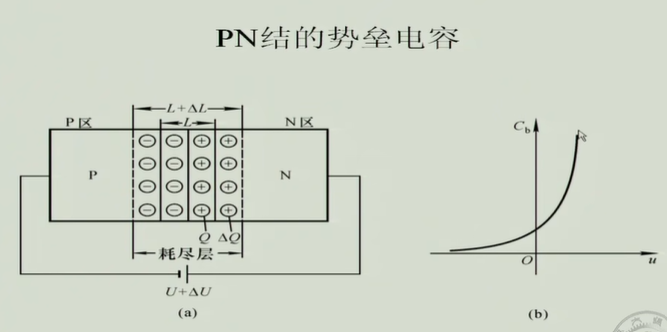
PN结的电容效应
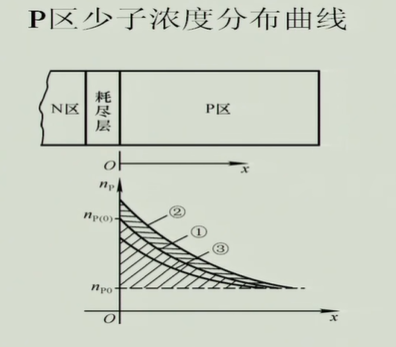
当正负极两边的电压变化时,中间的电量发生改变;
电压增高为2线,浓度增高,电压减小为3,浓度降低;
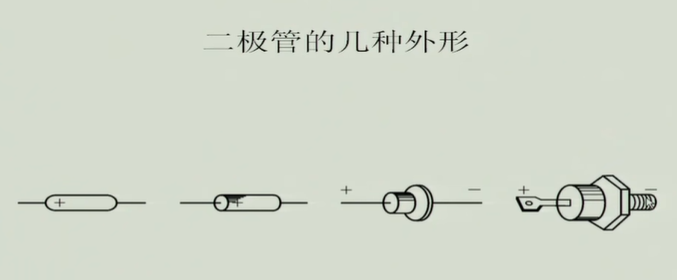
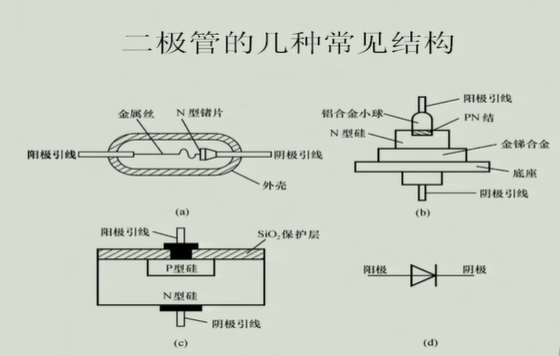
半导体二极管
常见结构
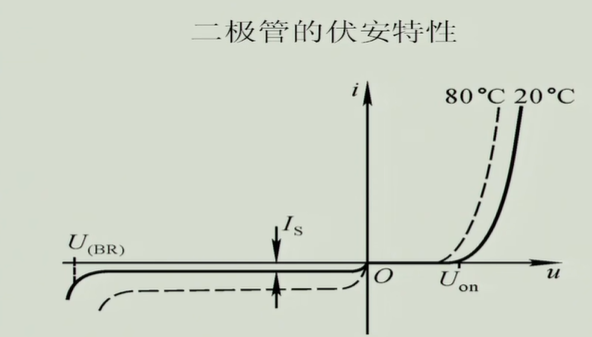
伏安特性
- 体电阻的存在,电流的PN结小;
- 反向电流大一些;
温度的影响
正向电流:温度升高,本证激发,粒子热运动增加,所以电压固定的时候,温度高的电流可定大,所以曲线往上走;
反向电流:温度升高,对少子影响大,饱和电流增加,所以曲线往下走;
二极管作用
- 单向导电性,规定电流流向,做整流器件;也可以稳压,但一般用反向的稳压
- 反向的饱和电流,简单的温度传感器;
- 反向截止电流,稳压二极管;
问:为什么稳压电路不用正向的电压稳压?
二极管的主要参数
- IF:工作的时候电流的最大流过电流,
- UR:最高反向电压,
- IR:反向电流(未击穿时),
- FM:最高频率(选高频电路的时候需要参考),
二极管的等效电路
2.b图为常用的等效模型
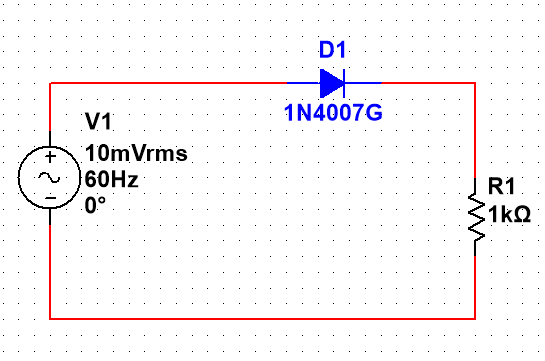
下面我们看二级管的几个应用:
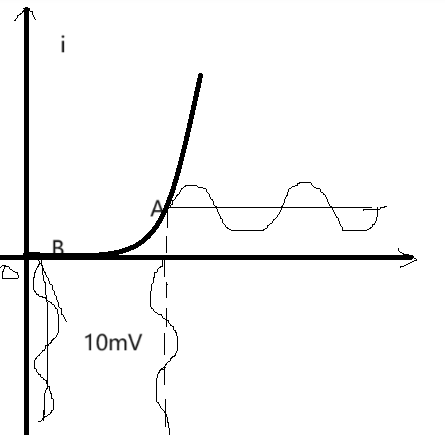
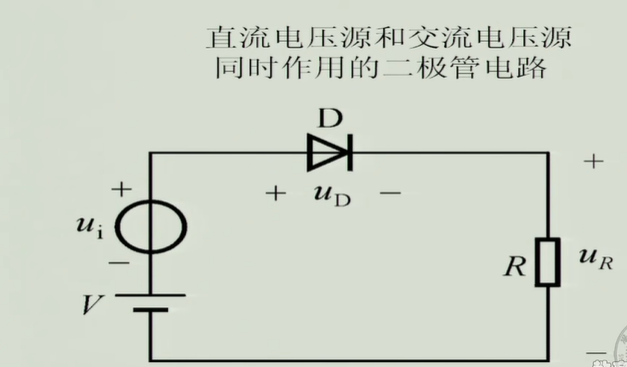
在上面的这个电路中我们假设交流电10mV,要想在$u_R$中测量出变化的电流那么需要加一个直流电压,将交流电抬高,曲线图如下:
上图B点的电压10mV升到A点,它们的关系是:$U_A=U_B+V$,那么此时就可以测量出$u_R$两端的变化的电流了。具体电路图如下:
最后得到的波形图是去掉Y轴的负半轴的正弦三角函数图像,也就是整流电路。
- 限幅电路
在分析这个电路时,要先判断正向导通和反向截止。
- 当$U_S-U_1<=Uon$的时候截止
- 当$U_S-U_1>=Uon$的时候导通
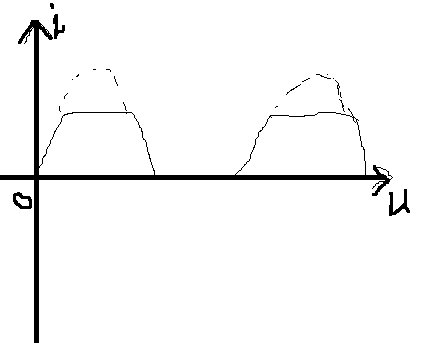
这时候的三角函数上半边会被割掉如下图: